静电场中的导体和电介质

茗与 Guderian 出品

静电感应：在电场的作用下导体上的电荷重新分布的现象

感生电荷：静电感应所产生的电荷（感生电荷代数和为零）

静电平衡：

静电平衡时导体上电荷分布：

静电平衡导体内各处的净电荷为零，导体自身带电或其感生电荷都只能分布于导体表面
静电平衡导体表面外附近的电场强度$E$的大小与该处该处表面上的电荷面密度$\sigma$的关系为$E=\frac{\sigma}{\varepsilon_0}$

静电屏蔽：

静电应用：

电容和电容器

孤立导体的电容： $\frac{Q}{U}=C$ ，$C$为电容，单位$F$（法拉），$1F={10}^6\mu F={10}^{12}pF$

电容器：$C=\frac{Q}{U_{AB}}$（两极板带电分别为$+Q$,$-Q$）

平板电容器：

圆柱形电容器：

$E=\frac{\lambda}{2\pi\varepsilon_0r}$（高斯定理）
$U_{AB}=\int_{R_A}^{R_B}{E\cdot d\ r=}\frac{\lambda}{2\pi\varepsilon_0}ln\frac{R_B}{R_A}$
$C=\frac{Q}{U_{AB}}=\frac{2\pi\varepsilon_0L}{ln\frac{R_B}{R_A}}$

球形电容器：

电容器并联：$C=\sum_{i=1}^{N}C_i$

电容器串联：$\frac{1}{C}=\sum_{i=1}^{N}\frac{1}{C_i}$

电介质：大量中性分子组成的绝缘体，可分为无极分子和有极分子

无极分子：外电场不存在时，分子正负电荷中心是重合的

有极分子：外电场不存在时，分子正负电荷中心不重合的，其电偶极矩称固有极矩

位移极化：在外加电场的作用下无极分子正、负电荷中心发生相对位移，形成的电偶极矩称为感生电矩

取向极化：在外加电场作用下分子的固有电矩受力矩作用，力图使分子旋转到与外场相同的方向上，温度越低极化效应越显著

注：取向极化是有极分子特有的；位移极化在任何电介质中都存在

电极化强度$P$：$P$等于单位体积内电偶极矩的矢量和，单位$C\cdot m^{-2}$，$P=\frac{\mathrm{\Sigma}p_i}{\mathrm{\Delta V}}$（$P$是宏观量）

极化电荷（束缚电荷）：电介质的某些部位出现因极化而产生的电荷（不是自由电荷）

注：物理性质均匀的电介质，极化电荷集中在电介质表面，电介质内没有静电荷；电介质的电极化程度越高，电介质表面的极化电荷面密度越大

退极化场：$E=E_0-E^\prime=\frac{E_0}{\varepsilon_r}$

有电介质时的高斯定理：

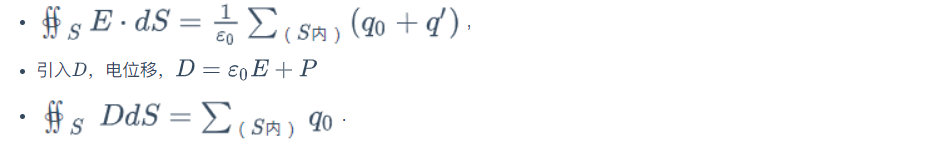
通过任意闭合曲面的电位移通量，等于该闭合曲面所包围的自由电荷的代数和

电场边界条件：在界面无自由电荷的情况下，界面两侧的

点电荷之间的相互作用能：$W_{int}=\frac{1}{2}\left(q_1U_{12}+q_2U_{21}\right)$

多个电荷体系的互能：$W_{int}=\frac{1}{2}\sum_{i=1}^{N}{q_iU_i}$

电荷连续分布带电体的静电能：

电容器的储能：$W_e=\frac{1}{2}QU_{AB}=\frac{1}{2}CU_{AB}^2=\frac{Q^2}{2C}$

能量密度：