模式匹配算法：KMP算法

图：北京航空航天大学

Guderian出品

模式匹配是数据结构中字符串的一种基本运算，给定一个字符串P，要求在某个字符串T中找出与字符串P相同的所有子串，这就是模式匹配。

模式匹配算法要解决的问题

detection ：P是否出现
location ：首次在哪里出现
counting ：共有几次出现
enumeration ：各出现在哪里？

绪论

KMP算法（全称Knuth-Morris-Pratt算法）是一种高效的模式匹配算法。在模式匹配算法中，常见的算法包括BF算法（朴素算法）、KMP算法、BM算法、RK算法、有限自动机算法、Horspool算法、Sunday算法。在这些算法中，最经典的算法非KMP算法和BM算法莫属。这两种算法都有一个共同点：抽象，理解难度大。实际上，KMP算法还有一个明显特点：会者不难。本文内容默认你已经明白BF算法的原理和不足（因此这部分内容将简单略过），展开讲述KMP算法的原理、优点和c++代码实现。相信你在学会KMP算法之后将会有一种“踏遍青山人未老，这边风景独好”的快意。让我们开始吧。

BF算法

BF算法的本质就是暴力搜索。既然要在串T中找出与串P相同的所有子串，那不妨找出串T中所有与串P长度相同的子串，在逐个判断这个子串是否与串P相同。具体的例子点击这里或者看下方的视频（讲得很形象了，应该不会有理解上的困难）。设strlen(T) == n, strlen(P) == m，则BF算法的预处理时间为$0$，匹配时间为$O(mn)$，总时间复杂度为$O(mn)$（简直是蜗速），在大部分应用场景中并不优秀。

KMP算法

更高的效率

容易看出BF算法的效率是十分蹩脚的，而它蹩脚的原因也很明显：在一次匹配尝试中，一旦失配（某一位匹配失败），就把串P整体向右移动一位。在模拟算法运行过程中，我们发现如果开始匹配时第一位就失配，那么只向右移动一位的确无可厚非，毕竟说不定移动一位之后就会匹配成功呢；但是如果已经匹配了串P的一部分了才失配，在向右移动一位之后，有时候（而且往往是经常）我们发现依然注定会匹配失败，也就是说在上次失败之后，向右移动一位再做尝试是根本不必要的，这种“只移动一位”的策略实际上造成了巨大的步骤浪费。那么有没有办法，把这些不必要的尝试舍弃，节约算法的运行时间呢？

此处我们需要考虑以下问题，以便对BF算法做出有效的改进：

为什么有一些尝试是注定徒劳的？
如何判断哪些尝试需要舍弃？
如果不是向右移动一位，又应该如何确定向右移动的位数？

在看完点击这里（还是上面那个链接）之后，前两个问题都能得到答案。在链接的视频讲解中，讲述者构造了一个前缀表数组prefix table来确定串P中每个从头开始的子串的最长公共前后缀（自身除外，以下省略此说明），一旦失配，就把串P向右移动到失配位置左侧子串的最长前缀处，使它们重叠，也就是把下图中的1号移动到2号位置，继续从当前位置匹配，如果当前位置为串T的结尾，则结束匹配。

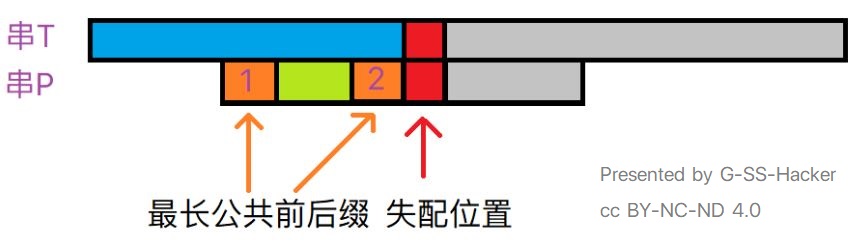
那么问题来了：为什么要把最长公共前缀移动至最长公共后缀的位置？这个移动距离能不能更短？能不能更长？

引理串的最长公共前后缀的最长公共前后缀是原串的次长公共前后缀。

证明略（逃

实际上，在BF算法的一次匹配过程中，一旦失配，就把串P整体向右移动一位再次尝试匹配。假设第一次匹配时在串P的第r + 1位失配，此时已经确定串P失配位置的前r项与串T相应位置元素匹配，也确定了串P失配位置的前r - 1项与串T相应位置元素匹配。那么第二次匹配成功，当且仅当在串P的前r项组成的子串中，前r - 1位字符组成的前缀和后r - 1位字符组成的后缀相同，即某一个公共前后缀长度为r - 1。也就是说，如果匹配失败向右移动s位，那么再次匹配成功的必要条件是串P在失配位置前的子串的某一个公共前后缀长度为r - s。如果串P在失配位置前的子串的最长公共前后缀长度就是r - s，匹配失败后向右移动了不足s位，这意味着移动距离过短，将会做一遍无用功。

如果移动距离过长，那就有可能会错过一个成功的匹配。如果匹配失败向右移动s位，那么再次匹配成功的必要条件是串P在失配位置前的子串的某一个公共前后缀长度为r - s。注意这里是必要条件而不是充分条件，在把串P向右移动的过程中，并不是在失配位置前随便放一个公共前后缀都能匹配成功，我们需要从最长公共前后缀开始尝试，逐步减少原失配位置前子串的长度，直到匹配成功或者串P在失配位置前子串最长公共前后缀长度变为0。

此处我们引入next[]数组来记录在失配时应该把串P的哪一位移动到当前位置。对于串P的第j + 1位的字符来说，next[j + 1]的意义是由串P的前j项的子串中最长公共前后缀的长度。next[]数组是KMP算法降低时间复杂度的关键，在预处理时就已经确定。下面介绍next[]数组求法。

next数组求法

如果你直接跳过了前面看到了这里，那说明你已经看了无数多参考资料，还是搞不懂next[]数组求法的原理，几乎走投无路了。但是，正如B站鬼畜区某神所言：

我们遇到什么困难也不要怕，微笑着面对它！消除恐惧的最好办法就是面对恐惧！坚持就是胜利！加油！奥利给！

回到正题。

先考虑求next[]数组的朴素算法：我们要求一个长度为l的串S的最长公共前后缀，因为自身除外，所以把串S复制一遍，产生一个串S'，并让串S'的第1位对齐串S的第2位，尝试匹配剩余l - 1位。若匹配成功，则剩余l - 1位就是串P的最长公共前后缀；若匹配失败，则把串S'向右移动1位，再次尝试，知道匹配成功或串S'已被移出串S的范围之内。

等一等，为什么这波操作如此熟悉？（战术后仰

是的，这就是所谓的“串P匹配自身”，有没有办法可以优化以上的朴素算法呢？

我们的任务是求出串P每一个由前j项元素组成的子串的最长公共前后缀的长度。假设串P从字符串下标1开始存储，规定next[1] = 0，并从第2位开始匹配。设用串P'匹配串P，当前匹配位置是串P'的第j + 1位，串P的第i位，如果失配，那么处理方法同上面介绍的一样，把串P'向右移动到失配位置左侧子串的最长前缀处，即令j = next[j]（思想：回溯），使它们重叠，即把下图中的1号移动到2号位置，继续从当前位置匹配；如果第j + 1位匹配成功，则更新串P前i位元素组成的子串的最长公共前后缀的长度为j，即令next[i] = j。

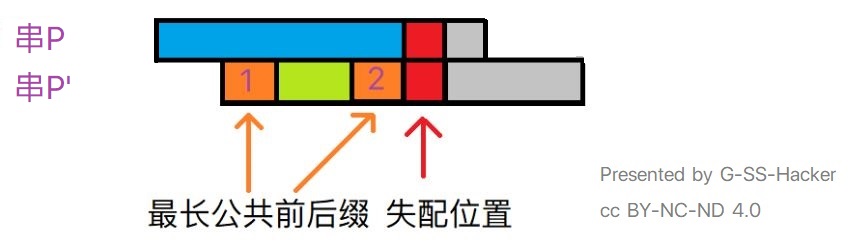
你已经明白了KMP算法的原理，那么不难推算出KMP算法的时间复杂度：预处理时间为$\Theta(m)$，匹配时间为$\Theta(n)$，总时间复杂度为$\Theta(m+n)$。与BF算法相比，KMP算法是一种优秀的模式匹配算法。

伪代码

KMP-MATCHER(T, P)

n = T.length
m = P.length

next = COMPUTE-PREFIX-FUNCTION(P)

j = 0
for i = 1 to n
	while j > 0 and P[j + 1] != T[i]
		j = next[j]
	if P[j + 1] == T[j]
		j = j + 1
    if j == m
    	print "Pattern occurs with shift" i - m
    	j = next[j]
    	
COMPUTE-PREFIX-FUNCTION(P)

m = P.length
let next[1..m] be a new array
next[1] = 0
j = 0
for i = 2 to m
	while j > 0 and P[j + 1] != T[i]
		j = next[j]
	if P[j + 1] == T[j]
		j = j + 1
    next[i] = j
return next

例题：KMP算法模版

题目描述

输入两个字符串$s1$和$s2$（皆从下标为$1$处开始存储），$s2$为$s1$的子串，输出$s2$在$s1$中所有出现位置的下标。

输入格式

第一行为$s1$，第二行为$s2$

输出格式

每行一个正整数表示s2在s1中出现的位置

输入样例

1 2	123456123 123

输出样例

1
2

1
7

说明/提示

$s1$和$s2$的长度在$1000000$之内
运行速度不能太慢

解题方法

//Presented by G-SS-Hacker
//cc BY-NC-SA 4.0
//Run on C++

#include <iostream>
#include <cstring>

using namespace std;

const int MAXN = 1000000 + 100;
const int MAXM = 1000000 + 100;

//next,x0,x1,y0,y1,index cannot be named to variables
int nxt[MAXM];	//nxt[i]表示字串1到i最长公共前后缀的长度
int len1, len2;
char s1[MAXN], s2[MAXM];

void pre()
{
	for(int j = 0, i = 2; i <= len2; i++)
	{
		while(j && s2[i] != s2[j + 1])
			j = nxt[j];
		if(s2[i] == s2[j + 1])
			j++;
		nxt[i] = j;
	}
}

void kmp()
{
	for(int j = 0, i = 1; i <= len1; i++)
	{
		while(j && s1[i] != s2[j + 1])
			j = nxt[j];
		if(s1[i] == s2[j + 1])
			j++;
		if(j == len2)
			cout << i - len2 + 1 << endl, j = nxt[j];
	}
}

int main()
{
	cin >> s1 + 1 >> s2 + 1;

	len1 = strlen(s1 + 1);
	len2 = strlen(s2 + 1);

	pre();
	kmp();

	return 0;
}

结束语

我们遇到什么困难也不要怕，微笑着面对它！消除恐惧的最好办法就是面对恐惧！坚持就是胜利！加油！奥利给！

【其他文章·数据结构】