图的表示

Guderian出品

绪论

对于图 $G=(V,E)$ ¹，可以用多种表示方法来表示，其中不同的表示方法分别适用与不同特点的图和对图进行不同的操作。在此介绍三种图的表示方法：邻接表、邻接矩阵和边集数组，并将呈现三种存图方法的C和C++代码实现。

存图方法

1.邻接矩阵

邻接矩阵是一种简单、易用但有较大局限性的存图方式。由于图是由点集和边集两部分组成，难以找到一种线性结构来同时表示两者，那么，由于每条特定的边都可由其两端顶点唯一确定（假设无重边），我们很自然地可以想到使用一个$|V|$ $*$ $|V|$的方矩阵$A = (a_{ij})$来表示，对于无权图，该矩阵满足：

$$a_{ij} = \left\{ \begin{array}{} 1, \ (i, j) \in E\\ 0, \ (i, j) \notin E \end{array} \right.$$

对于带权图，该矩阵满足：

$$a_{ij} = \left\{ \begin{array}{} w, \ (i, j) \in E\\ \infty \ or \ 0\ or-1, \ (i, j) \notin E \end{array} \right.$$

---

【例1】

无向带权图示例如下图所示：

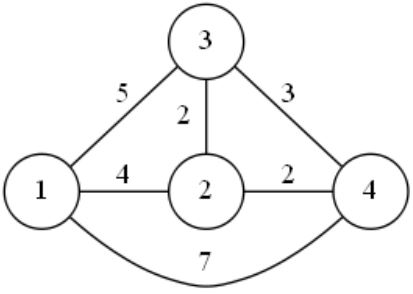
上图对应的邻接矩阵表示如图：

$$\mathbf{A} =\left( \begin{array}{ccc}a_{11} & a_{12} & a_{13} & a_{14} \\\\a_{21} & a_{22} & a_{23} & a_{24} \\\\a_{31} & a_{32} & a_{33} & a_{34} \\\\a_{41} & a_{42} & a_{43} & a_{44}\end{array} \right)\mathbf{} =\left( \begin{array}{ccc}\infty & 4 & 5 & 7 \\\\4 & \infty & 2 & 2 \\\\5 & 2 & \infty & 3 \\\\7 & 2 & 3 & \infty\end{array} \right)$$

---

//Run on C/C++
const int n = 4;  //n个顶点
const int inf = 0x3f3f3f3f;  //正无穷
int G[n][n] = {
	{inf, 4, 5, 7}, 
	{4, inf, 2, 2}, 
	{5, 2, inf, 3}, 
	{7, 2, 3, inf}
};

【例2】

有向带权图示例如下图所示：

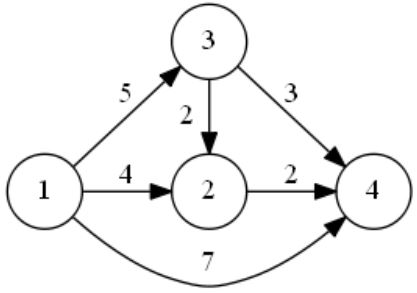
上图对应的邻接矩阵表示如图：

$$\mathbf{A} =\left( \begin{array}{ccc}a_{11} & a_{12} & a_{13} & a_{14} \\\\a_{21} & a_{22} & a_{23} & a_{24} \\\\a_{31} & a_{32} & a_{33} & a_{34} \\\\a_{41} & a_{42} & a_{43} & a_{44}\end{array} \right)\mathbf{} =\left( \begin{array}{ccc}\infty & 4 & 5 & 7 \\\\0 & \infty & 2 & 2 \\\\0 & 0 & \infty & 3 \\\\0 & 0 & 0 & \infty\end{array} \right)$$

---

//Run on C/C++
const int n = 4;  //n个顶点
const int inf = 0x3f3f3f3f;  //正无穷
int G[n][n] = {
	{inf, 4, 5, 7}, 
	{0, inf, 2, 2}, 
	{0, 0, inf, 3}, 
	{0, 0, 0, inf}
};

【例1】【例2】分别给出了无向无权图和有向无权图的邻接矩阵表示，不管一个图有多少条边，邻接矩阵的空间复杂度都为$O(V^2)$。

不难看出，无向图的邻接矩阵是一个对称矩阵。由于在无向图中，边$(u,v)$与边$(v,u)$表示同一条边，无向图的邻接矩阵$A$就是自己的转置，即$A = A^T$。在存储时，可以只存放主对角线及其以上的这部分邻接矩阵（即半个矩阵），从而将图存储空间需求减少几乎一半。

邻接矩阵表示简单、容易理解，对已知的边操作的效率高（插入、删除、查询的时间复杂度都是$O(1)$。但是邻接矩阵的缺陷在于其空间复杂度巨大，在稠密图上邻接矩阵可以取得较好的利用率，但是在稀疏图 ²上使用邻接矩阵将会造成大量内存空间的浪费，很容易导致内存溢出。因此，在使用邻接矩阵存图时一定要格外注意内存空间的限制，不可盲目追求简单而忽略了内存空间的优化。

---

2.邻接表

邻接表是一种具有高度鲁棒性 ³、适用于大多数情况的存图方法。对于图$ G = (V,E)$，其邻接表表示由一个包含$|V|$条链表的数组Adj[] ⁴所构成，每个顶点有一条链表。对于每个顶点$u\in V$，邻接表Adj[u]包含所有与顶点$u$之间有边相连的顶点$v$，即Adj[u]包含图$G$中所有与$u$邻接的顶点。邻接表本质上是使用链表存边，一条链表代表着一个点发出的所有边，通过链表存储和遍历和一个顶点相连的所有边，并根据实际应用情况选择是否存储边权。在C/C++中，实现邻接表的方法主要有两种：链式向前星和vector存图。

【例3】

有向带权图示例如下图所示：

上图对应的邻接表表示如图：

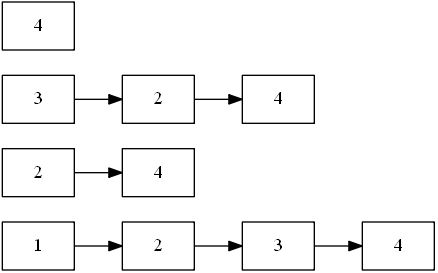
链式向前星存图法是利用了一种特殊的链表，这种链表具有普通链表链式存储的特征，但其插入新元素的方式却是“向前星”，即从链表表头插入元素，每次只更新表头，因此得名链式向前星。在使用链式向前星时，应很好的理解这种数据结构与普通链表的区别。

//链式向前星
//Run on C/C++
#include<iostream>
using namespace std;

const int n = 4, m = 6;  //n个顶点，m条边

struct edge
{
	int w, v, nxt;  //nxt指向同一个顶点发出的另一条边
}E[n];

int cnt = 0;
int head[m];  //假设从0号顶点开始存储

void add(int u, int v, int w)  //改变编号为cnt的边
{
	E[++cnt].v = v;  //出边指向v
	E[cnt].w = w;  //记录边权
	E[cnt].nxt = head[u];  //将其指向目前链表的表头（重要！）
	head[u] = cnt;  //将表头更新为目前的编号（重要！）
}

int main()
{
    add(1, 2, 4);
    add(1, 4, 7);
    add(1, 3, 5);
    add(3, 4, 3);
    add(3, 2, 2);
    add(2, 4, 2);
    return 0;
}

vector存图实际上是利用了一个不定长的链表该存储从一个顶点出发的所有边的情况，与普通链表类似，vector也是从链表的尾端进行插入操作，因此vector存图法在理解难度上比链式向前星要简单。然而由于C/C++语言的原因，使用vector存图实际使用的内存比链式向前星的要大，因此内存溢出的风险也会更大。

//vector存图，使用stl::pair版
//Run on C/C++
#include<iostream>
#include<vector>
using namespace std;

const int n = 4;  //n个顶点

vector<pair<int, int>> E[n + 1];  //int（first）为u，int（second）为v

void add(int u, int v, int w)
{
    E[u].push_back({v, w});
}

int main()
{
    add(1, 2, 4);
    add(1, 4, 7);
    add(1, 3, 5);
    add(3, 4, 3);
    add(3, 2, 2);
    add(2, 4, 2);
	
	for(int i = 1; i <= n; i++)
		for(int j = 0; j <(int)E[i].size(); j++)
			cout<<i<<" "<<E[i][j].first<<" "<<E[i][j].second<<endl;
	
	return 0;
}

//vector存图，使用结构体版
//Run on C/C++
#include<iostream>
#include<vector>
using namespace std;

const int n = 4;  //n个顶点

struct edge
{
	int v, w;
};

vector<edge>E[n + 1];

void add(int u, int v, int w)
{
    E[u].push_back({v, w});
}

int main()
{
    add(1, 2, 4);
    add(1, 4, 7);
    add(1, 3, 5);
    add(3, 4, 3);
    add(3, 2, 2);
    add(2, 4, 2);
	
	for(int i = 1; i <= n; i++)
		for(int j = 0; j <(int)E[i].size(); j++)
			cout<<i<<" "<<E[i][j].v<<" "<<E[i][j].w<<endl;
	
	return 0;
}

不管是用链式向前星存图还是vector存图，邻接表的空间复杂度都为$O(E + V)$。与邻接矩阵相比，邻接表的空间复杂度更小，空间利用率更高。但是邻接表使用链式结构存储边，这导致了对边操作的时间复杂度为$O(n)$，因此邻接表并不适用于需要频繁对边操作的情况；对于稠密图，邻接表的性能也不比邻接矩阵更占上风。然而，对于不需要频繁对边进行操作的稀疏图，使用邻接表存图比使用邻接矩阵存图可以期待更高的效率。综上，邻接表不失为一种性能优秀的存图方法。

---

3.边集数组

边集数组也是一种简单、易用但有较大局限性的存图方式。边集数组由一个一维结构体数组e[]构成，数组的每个数据元素由一条边的起点下标（u），终点下标（v）和权值（w）组成，如下图所示。不难看出，边集数组关注边的集合，而不关注点的集合。因此，使用这种存图方法在需要遍历图的边集时可以获得很高的效率，但是在遍历图的点集时效率简直是灾难。不论一个图有多少个顶点，边集数组的空间复杂度都为$O(E)$。

【例4】

有向带权图示例如下图所示：

上图对应的边集数组如下表所示：

	u	v	w
e[1]	1	2	4
e[2]	1	4	7
e[3]	1	3	5
e[4]	3	4	3
e[5]	3	2	2
e[6]	2	4	2

//Run on C/C++
const int m = 6;  //m条边

struct edge
{
	int u, v, w;
};

edge E[m] = {
	{1, 2, 4}, 
	{1, 4, 7},
	{1, 3, 5},
	{3, 4, 3},
	{3, 2, 2},
	{2, 4, 2}
};

据观察，这种存图方法主要用于实现最小生成树的Krusal算法，其他情况下较少使用。

---

¹. 图，graph，记为“G”；顶点，vertex，记为“V”；边，edge，记为“E”。 ↩

². 稠密图与稀疏图的判断标准：(1)定性分析：稠密图的边数非常接近于完全图（即$n(n-1)$），而稀疏图的边数比完全图少得多。(2)定量分析：边数多于$nlogn$的图为稠密图，边数少于$nlogn$的图为稀疏图。 ↩

³. 鲁棒性，robust，即健壮性 ↩

⁴. 邻接表，adjlist，记为”Adj” ↩