拓扑排序

图：索菲亚教堂

Guderian出品

拓扑是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的一个学科。它只考虑物体间的位置关系而不考虑它们的形状和大小。

AOV网

在工程领域，一个大规模工程常被拆分为多个子工程，这些子工程被称为活动（Activity），在有向图中以顶点（Vertex）表示活动，以有向边表示活动之间的先后关系，这样的有向图被称为AOV网（Activity On Vertex Network）。在AOV网中，如果出现了闭环，就意味着有若干个活动将被无限次重复，工程将永远无法完成；因此，一个具有实用价值的AOV网，必定是一个有向无环图（DAG，Directed Acyclic Graph）。

绪论

对于一个有向无环图$G=(V,E)$，其拓扑排序是其上顶点的一个线性排序：对于有向边$(u,v)\in E$，顶点$u$在排序中在顶点$v$的前面（如果$G$包含环路，则不可能产生一个线性排序）。可以将$G$上各顶点在一条水平线上从左向右排开，且图的所有边的指向也都是从左向右。拓扑排序并未各顶点上的排序，而是各顶点逻辑上的排序，这种排序可能有不止一种。在工程上，常把一个大规模工程的各个子工程抽象为一个AOV网，用拓扑排序解决工程的调度问题。下面用一个示例说明拓扑排序的具体应用：

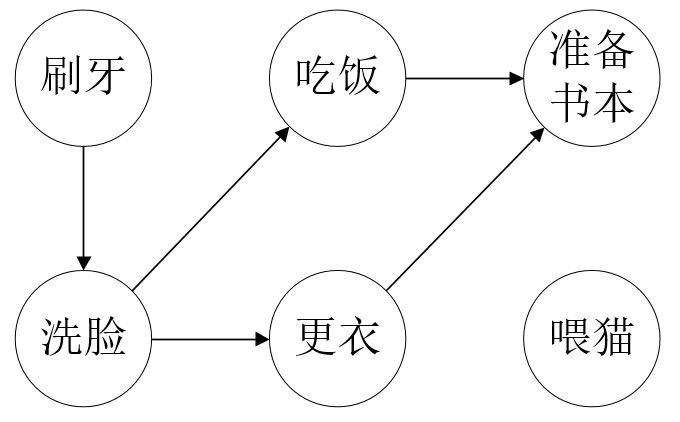
下图（a）表示的是某教授每天早上从起床后到上班前所发生的事情的AOV网。教授必须先完成某些活动，才能完成某些活动；而另一些活动则可以以任意次序完成。在图（a）中，有向边$(u,v)$表示的就是活动$u$必须在活动$v$前完成。图（b）将拓扑排序后的有向无环图在一条水平直线上展示出来。如图（b）所示，该有向无环图所有边的指向都是从左到右。

（a）

（b）

拓扑排序算法

1. 基于入度的拓扑排序

基于入度的拓扑排序算法，又被称为Kahn算法。以下摘选维基百科上关于Kahn算法的伪代码：

//TOPOLOGICAL-SORT(G)

L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges

while S is non-empty do
    remove a node u from S
    insert u into L
    for each node v with an edge e from u to v do
        remove edge e from the graph
        if v has no other incoming edges then
            insert v into S
if graph has edges then
    return error (graph has at least onecycle)
else 
    return L (a topologically sortedorder)

Kahn算法的基本思想是“走一步，看一步”。从以上伪代码不难看出Kahn算法的步骤：先统计所有顶点的入度，再把入度为零的顶点从图中分离出来，先放在集合$S$中，再从集合$S$中分别取出顶点放入线性表$L$中，然后把这个顶点指向的所有顶点的入度减1，并删除该顶点及所有与其相连的边。重复上述操作，直到所有顶点都被分离出来。若当集合$S$为空集时，线性表$L$中元素个数等于原来图中顶点的个数，则返回$L$，$L$中元素的排列即为该图的一种拓扑排序；若当集合$S$为空集时，线性表$L$中元素个数不等于原来图中顶点的个数，则意味着图中有闭环，返回错误信息，对图进行修改后再进行下一次拓扑排序。

对于图（a）的例子，首先我们找到入度为零的顶点有“刷牙”和“喂猫”，则把这两个顶点放入集合$S$中，$S=\{“刷牙”, “喂猫”\}$，$L=\varnothing$。

第一步、在$S$中选取”刷牙“并把该顶点从$S$中删除并放入线性表$L$中，”刷牙“与”洗脸“相连，删除相连的边，”洗脸“的入度减1，新的入度为0，把”洗脸“也放入$S$中。此时$S=\{“洗脸”, “喂猫”\}$，$L=“刷牙”$。

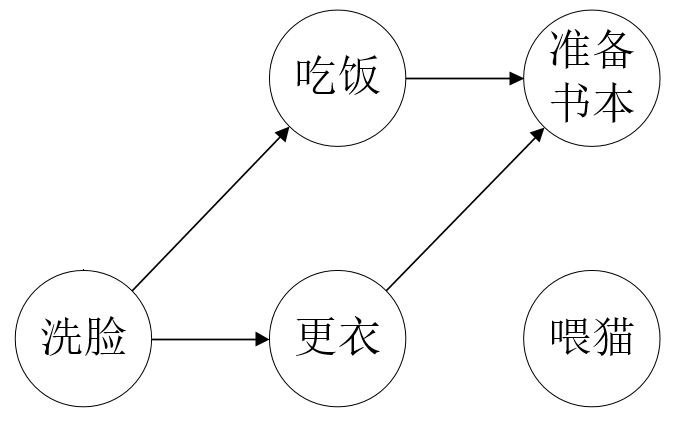
第二步、在$S$中选取“洗脸”并把该顶点从$S$中删除并放入线性表$L$中，“洗脸”与“吃饭”“更衣”相连，删除相连的边，”吃饭““更衣”的入度减1，新的入度为0，把”吃饭“”更衣“也放入$S$中。此时$S=\{“吃饭”, “更衣”, “喂猫”\}$，$L=“刷牙”\to“洗脸”$。

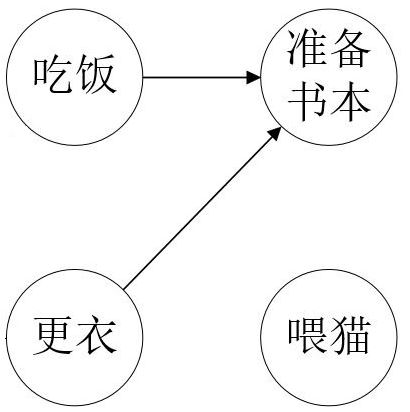
以此类推，第三步到第五步的结果分别如图（3）（4）（5）所示（第六步时$G=\varnothing$），采用同样的步骤，直至$S=\varnothing$，算法结束。

（3）

（4）

（5）

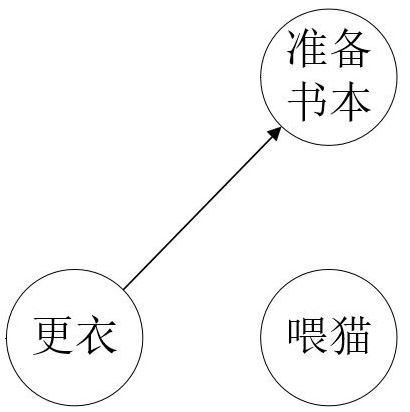
2. 基于深度优先搜索的拓扑排序

基于深度优先搜索的拓扑排序算法同样见以下维基百科上关于该算法的伪代码：

//TOPOLOGICAL-SORT(G)

L ← Empty list that will contain the sorted nodes
S ← Set of all nodes with no outgoing edges

for each node v in S do
    visit(v) 
    
function visit(node v)
    if v has not been visited yet then
        mark v as visited
        for each node u with an edge from u to v do
            visit(u)
        add v to L

这个算法的过程非常直观：先把出度为零的顶点从图中分离出来，放在集合$S$中，再从集合$S$中分别取出顶点，递归访问其父顶点，若该顶点未被访问，则标记为“已访问”；到达递归基础后，将当前顶点放入线性表$L$中，并逐步回溯。

下证基于DFS的拓扑排序算法生成的是有向无环图的拓扑排序：

在有向无环图$G=(V,E)$上运行DFS，只需证明对于任意一对顶点$(u,v)\in E$，$u$的返回在$v$之前即可。

对边$(u,v)\in E $，在调用DFS(v)时，对于即将访问的$u$，不外乎以下两种情况：

DFS(u)未被调用，即$u$未被mark，在当前路搜索路径的DFS树上，$u$是$v$的子节点。
DFS(u)已被调用，即$u$已被mark，则可知DFS(u)在另一条已经完成的搜索路径上返回。

对于这两种情况，$u$的返回都在$v$之前，得证。

例题：任务排序问题

题目描述

假定你需完成$n$项任务，这些任务之间并非独立，一项任务的执行当且仅当其所有前置任务已经被全部完成。

输入格式

输入的数据包含若干组样例，每个样例的第一行包括两个整数$n$和$m$。$n$是任务的数量，$m$是任务之间先后关系的数量。接下来有$m$行，每行有两个整数$i$和$j$，表示任务$i$的执行必须在任务$j$之前。

输入结束的标志是一组$n=m=0$的样例。

输出格式

对于每一组样例，在一行内输出$n$个整数，每两个整数之间用一个空格隔开，每一行数据表示一种可行的任务排序方案。

输入样例

输出样例

1 4 2 5 3

说明/提示

$1 \leq n \leq 100$

解题方法

解法一、Kahn算法

//Run on C++
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

const int MAXN = 110, MAXM = 110 * 110 / 2;

struct edge
{
	int v, nxt;
}E[MAXM];

queue <int> q;

int n, m, cnt;
int head[MAXN], in[MAXN];

void addedge(int u, int v)
{
	E[++cnt].v = v;
	E[cnt].nxt = head[u];
	head[u] = cnt;
}

void init()
{
	cnt = 0;
	memset(head, 0, sizeof(head));
	memset(E, 0, sizeof(E));
}		

int main()
{
	cin >> n >> m;
	while(n || m)
	{
		init();
		for(int i = 1; i <= m; i++)
		{
			int u, v;
			cin >> u >> v;
			addedge(u, v);
			in[v]++;
		}
		for(int i = 1; i <= n; i++)
			if(!in[i]) q.push(i);
		while(!q.empty())
		{
			int cur = q.front();
			q.pop();
			cout << cur << " ";
			for(int i = head[cur]; i; i = E[i].nxt)
				if(!--in[E[i].v]) q.push(E[i].v);
		}
		cout << endl;
		cin >> n >> m;
	}		
	return 0;
}

解法二、DFS

//Run on C++
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

const int MAXN = 110, MAXM = 110 * 110 / 2;

struct edge
{
	int u, nxt;
}E[MAXM];

queue <int> q;

int n, m, cnt;
int head[MAXN], out[MAXN];
bool flag[MAXN];

void addedge(int u, int v)
{
	E[++cnt].u = u;
	E[cnt].nxt = head[v];
	head[v] = cnt;
}

void init()
{
	cnt = 0;
	memset(head, 0, sizeof(head));
	memset(E, 0, sizeof(E));
	memset(out, 0, sizeof(out));
	memset(flag, 0, sizeof(flag));
}		

void dfs(int V)
{
	if(!flag[V]) 
	{
		flag[V] = true;
		for(int i = head[V]; i; i = E[i].nxt)
			dfs(E[i].u);
		cout << V << " ";
	}
}

int main()
{
	cin >> n >> m;
	while(n || m)
	{
		init();
		for(int i = 1; i <= m; i++)
		{
			int u, v;
			cin >> u >> v;
			addedge(u, v);
			out[u]++;
		}
		for(int i = 1; i <= n; i++)
			if(!out[i]) q.push(i);
		while(!q.empty())
		{
			dfs(q.front());
			q.pop();
		}
		cout << endl;
		cin >> n >> m;
	}		
	return 0;
}