
机器学习中的评价指标:F1-score
图:西雅图(Seattle)
Guderian出品
回顾:F1-score的计算过程
混淆矩阵(Confusion Matrix)
混淆矩阵也称误差矩阵,是表示精度评价的一种标准格式,用n行n列的矩阵形式来表示。
在机器学习领域,混淆矩阵用于衡量一个分类器的准确程度。对于二分类问题,将其样例根据真实类别和分类器的预测类别的组合划分为真正例$\mathrm{(True \, Positive)}$、假正例$\mathrm{(False \, Positive)}$、真反例$\mathrm{(True \, Negative)}$、假反例$\mathrm{(False \, Negative)}$四种情形。
对应混淆矩阵$\mathrm{(Confusion \, Matrix)}$如下表:
精确率(Precision)与召回率(Recall)
根据混淆矩阵,我们可以得到如下定义:
- 精确率$\mathrm{(Precision)}$ $\mathrm{P=\frac{TP}{TP+FP} \times 100\%}$,表示真实情况和预测结果皆为真/预测结果为真
- 召回率$\mathrm{(Recall)}$ $\mathrm{R=\frac{TP}{TP+FN} \times 100 \%}$,表示真实情况和预测结果皆为真/真实情况为真
F1分数(F1-score)
$\mathrm{F1=\frac{2}{\frac1{P}+\frac1{R}}=\frac{2PR}{P+R}}$F1分数($\mathrm{F1-score}$)即精确率与召回率的调和平均数($\mathrm{Harmonic \, Mean}$),比算术平均数($\mathrm{Arithmetic \, Mean}$)的评价效果更好。
直观理解为什么F1-score能评价模型优劣
在你训练的机器学习模型过程中,你往往希望能够兼顾精确率和召回率,并使用一个统一的单值评价指标来评价你的机器学习模型的训练效果。我们之所以使用调和平均而不是算术平均,是因为在算术平均中,任何一方对数值增长的贡献相当,任何一方对数值下降的责任也相当;而调和平均在增长的时候会偏袒较小值,也会惩罚精确率和召回率相差巨大的极端情况,很好地兼顾了精确率和召回率。
几何观点
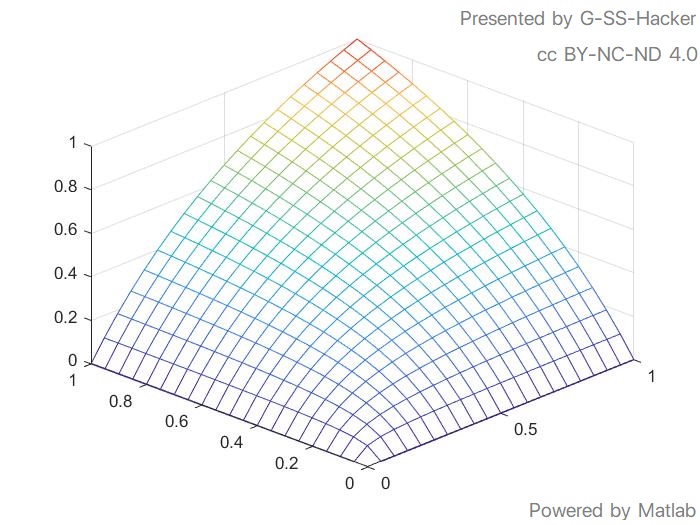
上图为函数图象$z=f(x, y)=\frac{2xy}{x+y}$。显而易见当$x=1$,$y=0$或者$y=1$,$x=0$时,$z=0$,说明调和平均惩罚精确率和召回率相差很大的极端情况。当$x<y$时,梯度$\mathrm{grad} \, z $在$x$方向增长比$y$方向快;当$y<x$时,梯度$\mathrm{grad} \, z$在$y$方向增长比$x$方向快,即调和平均在增长的时候会偏袒较小值。
代数观点
对函数$f(x, y)=\frac{2xy}{x+y}$,其图象关于平面$x=y$对称。分别求$f(x,y)$对$x$和$y$的偏导数:
$\frac{\partial f(x,y)}{\partial x}=\frac{2y^2}{(x+y)^2}$
$\frac{\partial f(x,y)}{\partial y}=\frac{2x^2}{(x+y)^2}$
当$x<y$时,$\frac{\partial f(x,y)}{\partial x}>\frac{\partial f(x,y)}{\partial y}$,梯度$\mathrm{grad} \, z $在$x$方向增长比$y$方向快;
当$y<x$时,$\frac{\partial f(x,y)}{\partial y}>\frac{\partial f(x,y)}{\partial x}$,梯度$\mathrm{grad} \, z$在$y$方向增长比$x$方向快,即调和平均在增长的时候会偏袒较小值。
可以看出,$\mathrm{F1-score}$是一种综合的评价指标,它要求总体高指标必须建立在同时满足高精确率和高召回率的情况之上。使得我们可以更方便快速地对不同模型进行比较,从而选择最优的那个模型。
Reference and lots of thanks:https://blog.csdn.net/otengyue/article/details/89426004